.._howto-dielectric-applied:

Dielectric Profile Calculations from Applied Field

This tutorial demonstrates how to calculate dielectric profiles using the “direct” method, where an applied electric field simulation is used to compute dielectric profiles for planar pores.

Note

In contrast to the fluctuation-dissipation formalism, this method necessitates one to run three simulations for a full determination of the dielectric profiles. First, one needs to run a simulation with no applied field for reference. Then, two additional simulations are run with an applied field in the parallel and perpendicular directions, respectively.

import matplotlib.pyplot as plt
import MDAnalysis as mda
import scipy.constants

import maicos

Next, we define the formulas for direct calculation of dielectric profiles. These are given by the following equations, first for the parallel component:

\[\varepsilon_{\parallel}^{-1} = \frac{\epsilon_0 E_\parallel + m_\parallel - m_{0, \parallel}}{\epsilon_0 E_\parallel}\]

and for the perpendicular component:

\[\varepsilon_{\perp}^{-1} = \frac{D - m + m_0}{D},\]

where \(D = \epsilon_0 E\) is the electric displacement field, \(m\)

unit_e = scipy.constants.e  # elementary charge in C
unit_a = scipy.constants.angstrom  # angstrom in m
epsilon_0 = scipy.constants.epsilon_0  # vacuum permittivity in F/m
unit_volt = 1


def direct_eps_par(m, m0, E=0.005):
    """Calculate the parallel dielectric profile."""
    m0 = m0 * unit_e / unit_a**2
    m = m * unit_e / unit_a**2
    E = E * unit_volt / unit_a
    eps0E = epsilon_0 * E  # vacuum permittivity times electric field
    return (eps0E + m - m0) / eps0E


def direct_eps_perp(m, m0, E=0.02):
    """Calculate the perpendicular dielectric profile."""
    m0 = m0 * unit_e / unit_a**2
    m = m * unit_e / unit_a**2
    D = E * unit_volt / unit_a * epsilon_0  # electric displacement field
    return (D - m + m0) / D

The key point of using MAICoS for this calculation is that it allows us to access the parallel and the perpendicular components of the polarization density, which are needed for the calculation of the dielectric profiles. For this, we need to run the dielectric module as we would do in the case of the fluctuation-dissipation formalism, once for the reference (no field) simulation and then twice for the applied field (parallel and perpendicular).

Warning

Because we measure the response (which might be only a small delta between reference and applied field simulations), we need to ensure that the bin locations are exactly the same for all three simulations.

Here, we have a universe with vacuum added in the z direction for the Yeh-Berkovitz correction which we remove before in order not to slow down the calculation with empty space.

def cut_yeh_box(ts):
    """Cut the simulation box, removing the vacuum for Yeh-Berkovitz."""
    dims = ts.dimensions
    ts.dimensions = [dims[0], dims[1], dims[2] / 3, 90, 90, 90]
    return ts


u = mda.Universe(
    "./graphene_water.tpr",
    "./graphene_water_nofield.xtc",
    transformations=[cut_yeh_box],
)
eps = maicos.DielectricPlanar(
    u.select_atoms("resname SOL"), bin_width=0.3, unwrap=False
)
eps.run(stop=100)
eps_means = eps.means

m0_perp = eps_means["m_perp"]
# take the x component, since the field is also applied in the x direction
# for the applied field simulations
m0_par = eps_means["m_par"][:, 0]

/home/docs/checkouts/readthedocs.org/user_builds/maicos/envs/518/lib/python3.13/site-packages/maicos/core/base.py:522: UserWarning: Your data seems to be correlated with a correlation time which is 4.89 times larger than your step size. Consider increasing your step size by a factor of 9 to get a reasonable error estimate.
  self.corrtime = correlation_analysis(self.timeseries)

This gives us the polarization densities for the reference simulation. The perpendicular density is one dimensional, the parallel density is two dimensional (x, y directions). For the applied field simulations, we need to take the parallel component in the direction of the applied field.

Now we can do the same for the applied field simulations.

u_par = mda.Universe(
    "./graphene_water.tpr", "./graphene_water_par.xtc", transformations=[cut_yeh_box]
)
eps_par = maicos.DielectricPlanar(
    u_par.select_atoms("resname SOL"), bin_width=0.3, unwrap=False
)
eps_par.run(stop=100)
m_par = eps_par.means["m_par"][:, 0]  # the field is applied in the x direction

u_perp = mda.Universe(
    "./graphene_water.tpr", "./graphene_water_perp.xtc", transformations=[cut_yeh_box]
)
eps_perp = maicos.DielectricPlanar(
    u_perp.select_atoms("resname SOL"), bin_width=0.3, unwrap=False
)
eps_perp.run(stop=100)
m_perp = eps_perp.means["m_perp"]  # the field is applied in the z direction

/home/docs/checkouts/readthedocs.org/user_builds/maicos/envs/518/lib/python3.13/site-packages/maicos/core/base.py:522: UserWarning: Your trajectory does not provide sufficient statistics to estimate a correlation time. Use the calculated error estimates with caution.
  self.corrtime = correlation_analysis(self.timeseries)
/home/docs/checkouts/readthedocs.org/user_builds/maicos/envs/518/lib/python3.13/site-packages/maicos/core/base.py:522: UserWarning: Your data seems to be correlated with a correlation time which is 2.38 times larger than your step size. Consider increasing your step size by a factor of 4 to get a reasonable error estimate.
  self.corrtime = correlation_analysis(self.timeseries)

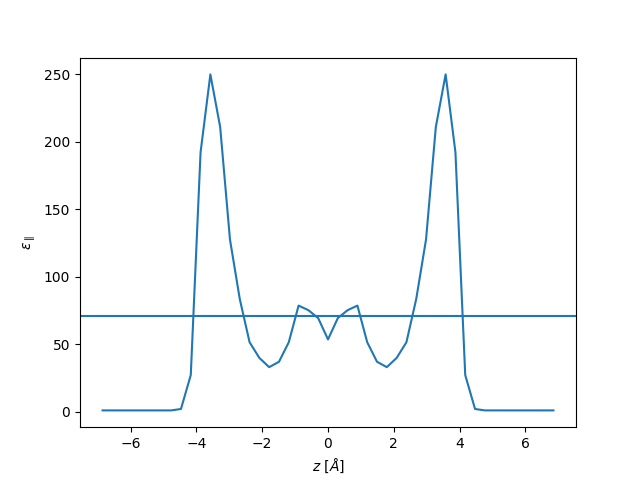
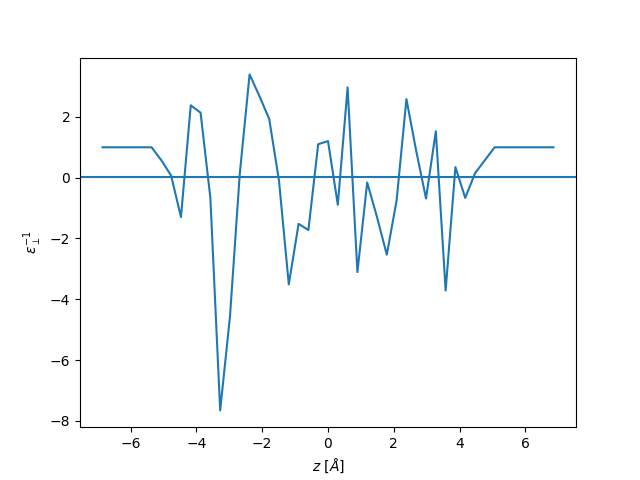
This allows us to calculate the dielectric profiles using the formulas defined above. THe example data was calculated for an applied field of strength 0.005 V/A in the parallel direction and 0.02 V/A in the perpendicular direction.

z = eps.results.bin_pos

eps_par = direct_eps_par(m=m_par, m0=m0_par, E=0.005)
eps_perp = direct_eps_perp(m=m_perp, m0=m0_perp, E=0.02)

If we apply a field we introduce asymmetry in the system, so it is good practice to symmetrize the profiles. This way the profile will be the same as those determined from fluctuation-dissipation formalisms, which assume perfect symmetry. Because of the short trajectories, we use this only for the parallel profiles, which converge much faster than the perpendicular. Still, we provide the code to symmetrize the perpendicular profiles as well.

eps_par = (eps_par + eps_par[::-1]) / 2
# eps_perp = (eps_perp + eps_perp[::-1]) / 2

plt.plot(z, eps_perp, label="perpendicular")
plt.axhline(1 / 71)

plt.ylabel(r"$\varepsilon_{\perp}^{-1}$")
plt.xlabel(r"$z$ [$\AA$]")
plt.show()

plt.plot(z, eps_par, label="parallel")
plt.axhline(71)
plt.xlabel(r"$z$ [$\AA$]")
plt.ylabel(r"$\varepsilon_{\parallel}$")
plt.show()